����ã�θ��漼�Ǥϡ�SNDM���Ѥ���ȾƳ�κ�����ǥХ�����ɾ�����ѤˤĤ��Ƥθ����ԤʤäƤ��ޤ���SNDM��Ȥ���ȾƳ�Τ�¬���Τ�������ʬ����Τ���Ҳ𤷤����Ȼפ��ޤ���
ȾƳ�ΤȤ�
���ޤ���ȾƳ�ΤˤĤ����������ޤ��礦��ʪ���ˤϤ���������ʬ�ब����ޤ������ŵ���ή���䤹����Ƴ��Ψ�ˤ����ܤ����ή���פ����
- ��°
- ȾƳ��
- �����
��ʬ�����ޤ����Ĥޤ�ȾƳ�ΤȤϡ����ŵ����°�ۤɤ�ή���ʤ���������ή���ʤ��櫓�ǤϤʤ�������Ⱦü��Ƴ��Ψ����ġˡ�ʪ���Ǥ����ʤ�Ȥ�����
Ⱦü��ʪ���Ǥ��������Ρ�����Ⱦü�ɤ�ʪ���ʤ��˳������äƤ���ѥ������������á����ޡ��ȥե����¸�ߤ��ޤ���ȾƳ�ΤκǤ���פ������ϡ�Ƴ��Ψ�ߤ��Ѳ������뤳�Ȥ��Ǥ���Ȥ��������Ǥ���������������Ѥ��ơ��ŵ���ή���Ū�ʥ����å�����뤳�Ȥʤ����ߤ����椹�뤳�Ȥǡ�����ԥ塼����Ϥ�Ȥ����Żҵ����ư��Ƥ��ޤ���
��ȾƳ�Τ��ŻҤ�ή������椹�����ʤϰ���Ū��ȾƳ�ΥǥХ����Ȥ��Ż����ʤʤɤȸƤФ�ޤ����Ǥ�ͭ̾�ʤ�Τϥ��������ɤȥȥ�����Ǥ���ȾƳ�ΥǥХ�����¸����������˽��פʤΤ�n��ȾƳ�Τ�p��ȾƳ�ΤǤ���n��ȾƳ�ΤȤ��ŻҤ�˭�٤��ŵ���Ƴ���ŻҤ˻��ۤ���Ƥ���ȾƳ�Τǡ�p��ȾƳ�Τϥۡ��뤬˭�٤��ŵ���Ƴ���ۡ���˻��ۤ���Ƥ���ȾƳ�ΤǤ���ȾƳ�ΥǥХ�����������ư��뤿��ˤ�n��ȾƳ�Τ�p��ȾƳ�Τ�Ŭ�ڤ����֤���Ƥ���ɬ�פ�����ޤ�����ã�����椷�Ƥ���SNDM��Ȥ���ȾƳ�ΥǥХ������n��ȾƳ�Τ�p��ȾƳ�Τ�ʬ�ۤ�ܺ٤�ʬ�Ϥ��뤳�Ȥ���ǽ�Ǥ�����¬������äƤʤ���̣���ʡפȻפ��ͤ��뤫�⤷��ޤ���ȾƳ�ΥǥХ������n����p����ʬ�ۤ�¬�뵻�ѤϥǥХ�����ȯ�ˤ��������˽��פ����ǤǤ����ǥХ�����ȯ�ˤ����ƤϾ�ˡ�����������Ƥ���Τ��פȤ����������ư��ʤ������ϲ����פȤ��ä����꤬�Ĥ��Ʋ��ޤ������Τ褦�ʵ�����褹��ˤ�ľ�ܹ�¤��¬�äƤ��ޤ��Τ���ƻ�Ǥ����äˡ���ǯ��CPU��������ɽ������絬�Ͻ��Ѳ�ϩ��LSI�ˤ������ι�¤���������٤ǡ��ȥ����1�Ĥ���ˡ��20nm���٤Ǥ��������ޤǾ������ʤ��¬����������ʤ�ޤ���SNDM�Ϥ��Τ褦�����٤ʥǥХ����ι�¤��ʬ�ϤǤ���ݥƥ����äƤ��ޤ���
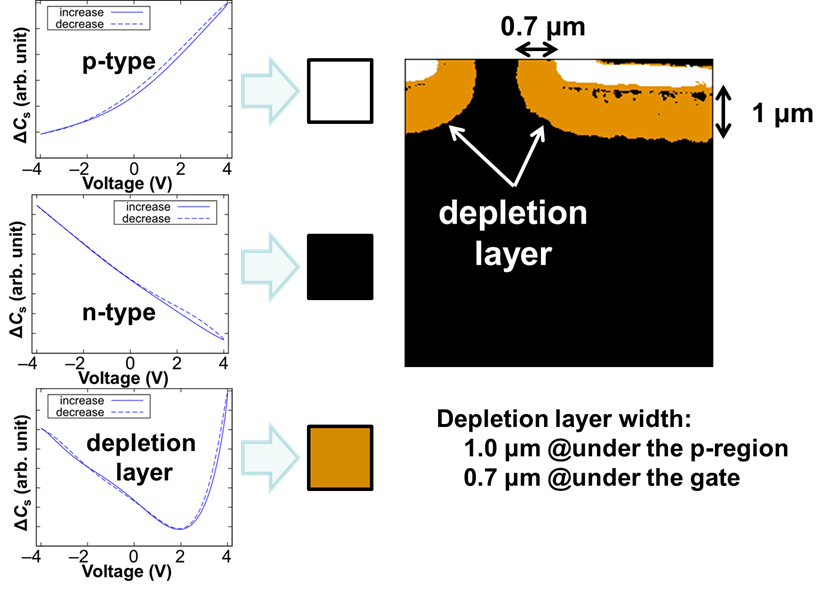
��SNDM�����̤��Ű����Ф��������¬��ץ����ָ��������Ȥ������Ȥ�SNDM��������ʬ���äƤ����������Ȼפ��ޤ���ȾƳ�Τ��������̤��Ű��ˤ�ä��Ѳ����뤿��SNDM��¬�꤬��ǽ�Ǥ�����1�Τ褦�ʡ����ʪ���Ŷˤ�p��ȾƳ�ΤǶ��������ѥ�����ͤ��ޤ��礦��
��1(a)�ξ��ˤϡ���������C��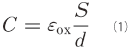
��ɽ����ޤ���
�Ȥ�������������Ű�����ä���ȡ����Ų٤���ĥۡ�����Ŷ�1����ȿȯ����Ʊ��ꡢ�Ŷ�1�β��˥ۡ��뤬¸�ߤ��ʤ��ΰ�ʶ�˳�ءˤ�����夬��ޤ���
������ʬ������Τ�Ʊ���ʤΤǡ���������C��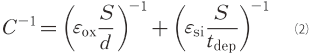
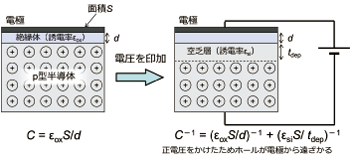
��1��MOS����ѥ���
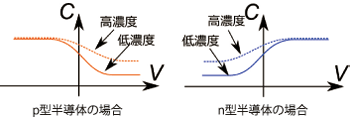
��2��ŵ��Ū��CV������
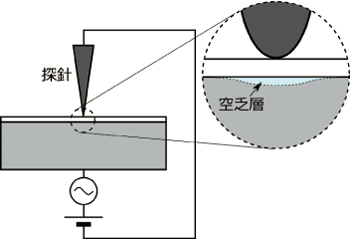
��3��õ�ˤ��Ѥ��������ΰ��C-V¬��
��ɽ����ޤ����Ĥޤꡢ�Ű�����ä������Ȥ��������̤��������ʤä��櫓�Ǥ���n���ξ��ϥ����䤬���Ų٤���ļ�ͳ�ŻҤʤΤǤ��εդǡ����Ű�����ä�������̤��������ʤ�ޤ���
��ñ��n����p���Ȥ��������ǤϤʤ��ơ��������ǻ�١�n���ʤ鼫ͳ�ŻҤ�ǻ�١�p���ʤ�ۡ����ǻ�١ˤ��Τ뤳�Ȥ��ǽ�Ǥ���ǻ�٤��Ű����Ф� �����̤α����ζ����˱ƶ���Ϳ���ޤ���ǻ�٤��⤯�ʤ�ۤ�ȾƳ�Τ϶�°�˶�ʤ뤿�����̤��Ѳ��Ͼ������ʤ�ޤ��ʶ�°�Ŷˤ�Ͷ���Τ������Ū�ʥ��� �ѥ����˶�Ť��ȹͤ����Ǽ�����䤹���Ȼפ��ޤ��ˡ����Τ褦�ˡ��Ű������̤δط���Ĵ�٤��n����p���ʤ�ȾƳ�Τ��������Τ뤳�Ȥ��Ǥ��ޤ������Τ褦 ��¬���CV¬��ȸƤӡ�ȾƳ�Τ�ʬ��Ǥϰ���Ū��¬��ǡ�ȾƳ�ΥǥХ����ζ��ʽ�����ߤ��ɬ���ܤäƤ��ޤ������ʽ�ʤɤǾҲ𤵤�Ƥ���ŵ��Ū��CV �����֤��2�˼����ޤ�����
�����ơ�SNDM�ǹԤ�¬��ϴ���Ū�ˤ�CV¬��Ǥ���������SNDM�ξ��ϡ���1���Ŷˤ��3�Τ褦�˱Ԥ���°õ�ˤ��֤������ƶˤ���������� ���CV¬���Ԥ��ޤ���â��SNDM�ξ�硢����C��¬�ꤹ��櫓�ǤϤʤ��������˸�ή�Ű�����ä��뤳�Ȥ����̤��Ű����Ф��������dC/dV�ˤ�¬ �ꤷ�ޤ�����2����ʬ����褦�ˡ�dC/dV�������礭����ȾƳ�ΤΥ�����ζ�����ǻ�٤��б�����Τǡ�SNDM������p����n����ʬ�ۤ��Τ뤳�Ȥ� �Ǥ��ޤ���
�������漼��ȾƳ�ΥǥХ���ɾ���˴ؤ��ƹԤʤäƤ����ʸ����
- �ǥХ������n����p����ʬ�ۤ�¬��
- Flash��������Ѥ��줿�Ų�ʬ�ۤ�¬��
- SiCȾƳ�ΥǥХ����Υ���ꥢʬ��¬��
- 2�����Żҥ����η�¬
- ���ꥳ��ñ�뾽�������Ӥη�¬
- Ķ�⼡������������Ͷ��Ψ������ˡ��SHO-SNDM��
- �ɽ�DLTSˡ�ˤ��MOS���̥ȥ�åפ�ʬ�۷�¬
- �����ء�2������ȾƳ�ΤΥ���ꥢʬ�۴ѻ�
��ʬ�����ޤ������줾��ˤĤ��Ʒ�̤ΰ�����ƾҲ𤷤ޤ���
�ǥХ������n����p����ʬ�ۤ�¬��
�������������������������Ƥ��Τ�ΤǤ���ȾƳ�ΥǥХ��������Ǥ��ơ���4�˼������褦�����̤�SNDM��¬�ꤷ�ޤ�����5�ϼºݤ˥ȥ���� �����̤�¬�ꤷ����ΤǤ�����������Ƥ����������ʬ�����̤�100 nm�ˤ������ʤ������ʥȥ�����Ǥ��������ι�¤�����Ƥ˲Ļ벽����Ƥ��ޤ���
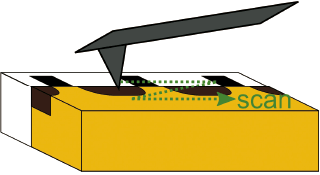
��4���ǥХ������̤Υ�����ʬ��¬��
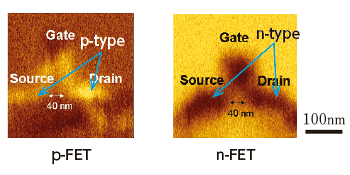
��5��FET���̤�SNDM��
Flash��������Ѥ��줿�Ų�ʬ�ۤ�¬��
�����ι��ܤϡ����ι��ܤȿ�ʬ��äƸ����뤫�⤷��ޤ���CV¬���Ԥ��Ȥ��������Ѥ��ޤ���
¬����ä��������ˤޤ���Flash����ˤĤ��ƴ�ñ���������Ƥ����ޤ���Flash����Ȥ���̾���Ϥߤʤ��ȤäƤ���USB�����ѥ������
SSD�˻Ȥ��Ƥ��뤿�ᤴ¸�Τ�����¿���Ȼפ��ޤ����ޤ����������Ӥ���ʬ����褦�ˡ�Flash������Ÿ����ڤäƤ�ǡ������ä��ʤ����Դ�ȯ
���˥���Ǥ���Flash�����1��1�ĤΥ��ꥻ����Ų٤��Ĥ�����뤳�ȤǾ�������ޤ�������ȡ����β��ˤ���ȥ�����Υ����Ȥ��Ű���
�����ä����֤ˤʤꡢ�ȥ������ư�������Ѳ����ޤ������Τ���ƥ��ꥻ����Ų٤��ߤ뤫̵������Ƚ�̤Ǥ��ޤ������Τ��ᡢ���ꥻ��ˤɤΤ褦����
�٤��ߤ����Ƥ��뤫�������ư��˽��פǡ����Ѥ��줿�Ų٤�ʬ�ۤ�¬�ꤹ�뤳�Ȥϥ������ǽ����夹�뤿��˽��פȸ����ޤ���
�������֤���Ĺ���ʤ�ޤ�������¬����ä����ޤ�������¬��ǤϥǥХ��������̤�¬�ꤹ��ΤǤϤʤ�����6�˼������褦�˾夫��¬�ꤷ�ޤ����Ų٤�����
����Ƥ�����ꥻ��Ǥϡ����Ѥ���Ƥ����Ų٤�����ȾƳ���ؤ��ų���ڤܤ�����CV�����֤��Ѳ����ޤ���ȾƳ�ΥǥХ����ζ��ʽ��Ȼ�������θ���
�Ų٤�MOS��������Ϳ����ƶ�����Ƥ���Ȼפ��ޤ����������Ʊ�ͤθ��̤Ǥ��ˡ������Ѳ��Ф��뤳�Ȥ����Ѥ���Ƥ����Ų٤ζ������̡�ʬ�ۤ���
�뤳�Ȥ��Ǥ��ޤ�����7��¬���̤ΰ���Ǥ������Ѥ��줿�Ų٤�¸�ߤ������˱Ǥ��Ф���Ƥ��ޤ���
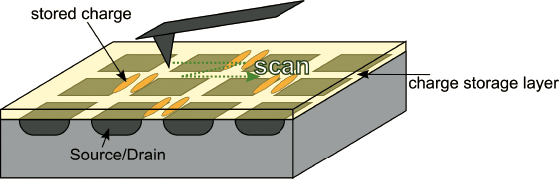
��6��Flash����������Ų�ʬ�ۤ�¬��
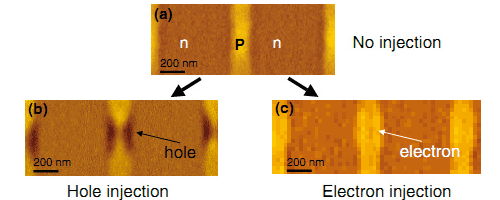
��7��MONOS��Flash����ˤ����������Ų�ʬ�ۤ�¬����[1]
SiCȾƳ�ΥǥХ����Υ���ꥢʬ��¬��
SNDM��ʬ�ϲ�ǽ�ʤΤ�SiȾƳ�ΥǥХ��������ǤϤ���ޤ��� ���̤�¬�꤬���ȸ����Ƥ��������⤤�������̴��٤Τ�������¬���ǽ�Ǥ��� ú�������ǡ�SiC��ȾƳ�ΥǥХ����Υ���ꥢʬ�ۤ�Ļ벽�������Ҳ𤤤����ޤ���
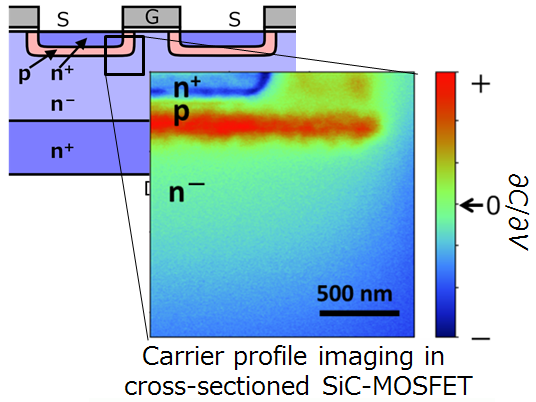
��8���ķ�SiC-MOSFET������¬��η��
�����ޤǤ��ŵ�Ū���Żߤ����ǥХ����Υ���ꥢʬ��¬��Ǥ������� �����ȡ��������֤��Ű�����ä����Ȥ��ε�ư��Ļ벽���뤳�Ȥ�Ǥ��ޤ��� �����ȡ��������֤�100 Hz���٤θ�ή�Ű�����ä��ƾ��֤� ��9�ˤ��������ȤǰϤޤ줿�ΰ��¬�ꤷ������ꥢʬ�ۤΥ����ȥХ�������¸����¬�ꤷ�ޤ����� ��10�Ϸ�̤�ư���ɽ��������ˤʤ�ޤ���
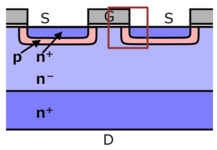
��9�����̥���ꥢʬ�ۤΥ����ȥХ�������¸��¬�ꥨ�ꥢ

��10�����̥���ꥢʬ�ۤΥ����ȥХ�������¸��¬��η��
��10�κ����ɽ������Ƥ�����ͤϥ����ȡ����������Ű��Ǥ��� ������Ǥ��֤��ΰ褬p�����ΰ衤�Ф��ΰ褬n�����ΰ��ɽ���Ƥ��ޤ��� �����ȡ����������Ű��˱����ƥ���ꥢʬ�ۤ��Ѳ����Ƥ����ͻҤ�Ļ벽���뤳�Ȥ��Ǥ��ޤ����� �����ǾҲ𤷤���Ǥ�FET������ʥ���ͥ뤬���������ˤޤǤϸ����Ƥ��ޤ��� ʸ��2�˥���ͥ�����ޤǤ�Ļ벽������̤��Ǻܤ���Ƥ��ޤ���
2�����Żҥ����η�¬
AlGaN/GaN �إ�ȡ�high-electron mobility transistor�ˤϥϥ��ѥ������ȥǥХ����Ȥ��ƴ��Ԥ���Ƥ��롥AlGaN/GaN �إƥ���¤�γ��̤ˤϤ��줾��κ������ʬ�ˤ���Ϣ³���������褦��2�����Żҥ�����ͯ���Ф�����2�����Żҥ�����ꥢ�Ȥ������ŻҰ�ư�٤Υȥ�� ���������¸�����Ƥ��롥����2�����Żҥ����θ������������������ޤǤ����¶��֤Ǵ�¬����Τ����ä��� ����SNDM�Ϥ������������Ѳ����Ф���ⴶ��������������2�����Żҥ����Τߤʤ餺ʬ�ˤ��S/N��Ǵ�¬��ǽ���롥 ���ޤ�AlGaN/GaN�إƥ���¤�γ�ǰ���¤Ӥ�SNDM�Ƿ�¬����ʬ�˵ڤ�2�����Żҥ����ΰ켡���ץ��ե��������
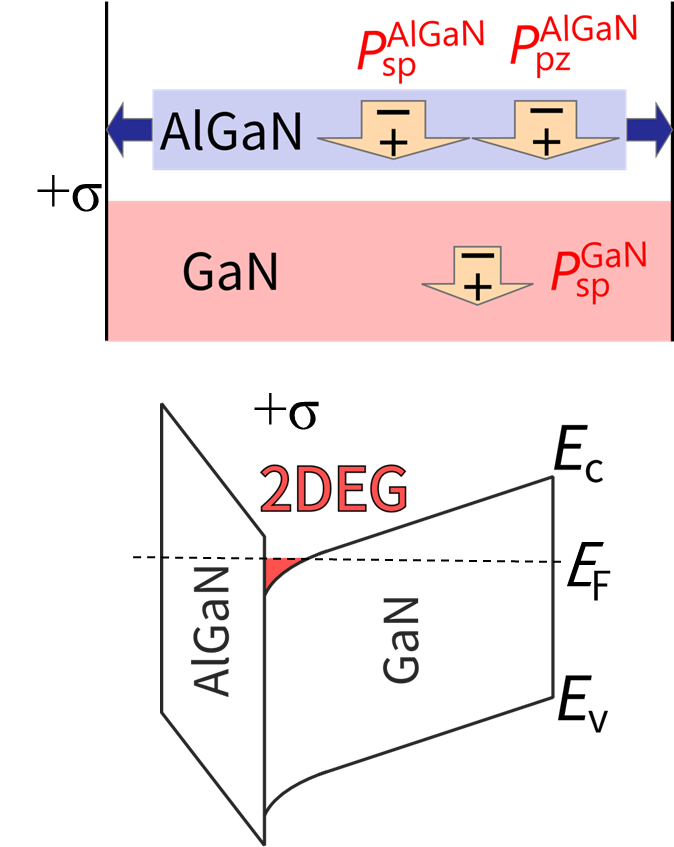
��11��lGaN/GaN�إƥ���¤�γ�ǰ�ޡ�����EC, EV,�ڤ� EF�Ϥ��줾����Ƴ��ü�����Ż���ü�ڤӥե���ߥ�٥�����ޤ� +�Ҥ�AlGaN/GaN �����Ǥ�ʬ�ˤ���Ϣ³ʬ���������륷�����Ų٤Ǥ��롥
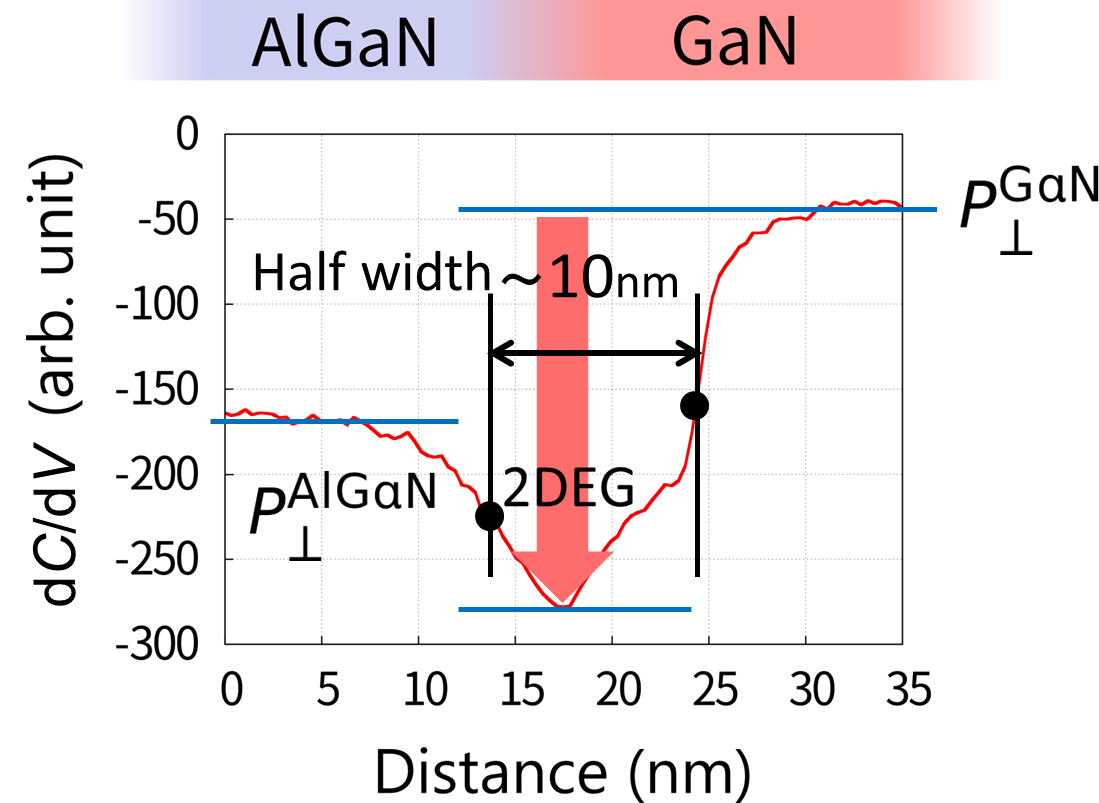
��12����¬���줿AlGaN/GaN�إƥ���¤��SNDM����Υץ��ե����롥
���ꥳ��ñ�뾽�������Ӥη�¬
���ꥳ��(Si)�������Ӥ�ȯ�Ÿ�Ψ�ϥ��ߥå���Υɡ��ѥ��ʬ�ۤ��礭����������롥�������������ӤΥ��ߥå��ϸ��εۼ���Ψ��夲�뤿��ԥ�ߥåɾ� �Υƥ������㹽¤��Ȥ뤿��Υɡ��ѥ��ʬ�ۤ��¬���뤳�Ȥ����Ȥ���Ƥ�����������SNDM���Ѥ��ƥ��ꥳ���������ӤΥ��ߥå���Υɡ��ѥ�� �ʥ���ꥢ��ʬ�ۤ��¬���Ƥߤ������η�¬�ˤ� SNDM (dC/dV) ˡ�ڤӥ���ꥢǻ�٤��Ф��뿮�涯�٤ΰ���ؿ������ݾڤ���Ƥ���dC/dz-SNDM ˡ������Ū���Ѥ����� ���ʾ��Υɡ��ѥ��ǻ��ʬ�ۤ����ɸ�ॵ��ץ���������Ӥ����̥���ץ��Ʊ����CMP���ᤷ�����Υǡ�������Ӥ��뤳�Ȥˤ�ꥨ�ߥå���Υ���ꥢǻ�� ������ɾ����Ԥä������η�̤��13�ˤޤȤ�Ƽ�����������3�����Υƥ������㹽¤�Ƥ��륨�ߥå���Υ���ꥢǻ�٤�����Ū�˷�¬�����ǽ�η�¬ ��Ǥ��롥
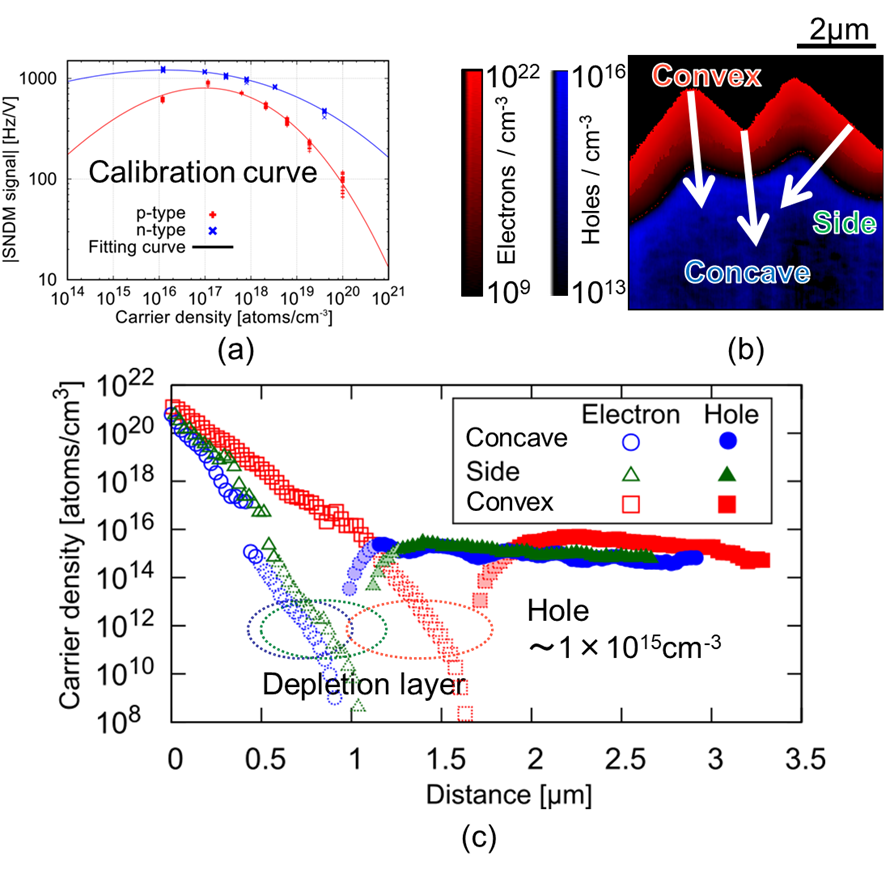
��13��(a) ɸ�ॵ��ץ���Υ���ꥢǻ�٤�SNDM����δط�����������. (b) ���ߥå���Υ���ꥢǻ�٤�����2����ʬ��(c) ����ꥢʬ�ۤΥ饤��ץ��ե�����.
Ķ�⼡������������Ͷ��Ψ������ˡ��SHO-SNDM��
��ǯdC/dV����Τߤʤ餺���ι⼡��ޤǼ�����ȾƳ�κ�����ǥХ����˴ؤ���¿����ʪ������������Ķ�⼡������������Ͷ��Ψ������ˡ��SHO- SNDM�ˤ���ȯ���줿�� �ܼ�ˡ���Ѥ���ȷ�¬�ԥ�������˶ɽ�Ū��C-V����������������衤ȾƳ�Τζ������˳�ؤ�ʬ�۷�¬����ñ�ˤǤ�������MOS���̷�¬��Ŭ�Ѥ�������� �˥ȥ�åפ��줿����ꥢ��Dit��ʬ�۷�¬����ǽ�ˤʤ������β���ǽ�Ϥ����ʤ˸��夹�롥 ���θ����ޤ�SNDM�δ��ܸ����ޤȶ��˿�14�˼�����SHO-SNDMˡ��Ԥ����ˤϥޥ������ͥ���å�����פ��Ѥ������Ȥ����Ĵ�������̾� 6�������˼����������������Ѳ���������롥���˻��֤����ѿ��˼�ꦤC-V������ԥ����뤴�Ȥ˺ƹ������롥�ܼ�ˡ���Ѥ�SiC-DIMOSFET�� ���̷�¬��Ԥä����ƹ�Ĵ�������15�˼����������Υǡ����ϳƥԥ�������ι�Ĵ����ʬ���礭�����Ƥ��ꡤ������Ѥ��ƥԥ��������C-V������� ����������C-V�����η���ñĴ���äǤ���Ф��Υԥ������p����ñĴ�����Ǥ����n����V���Ǥ���ж�˳�ؤ�Ƚ�ꤵ�졤��̿�16�˼����褦�ʶ�˳��ʬ �����������������롥
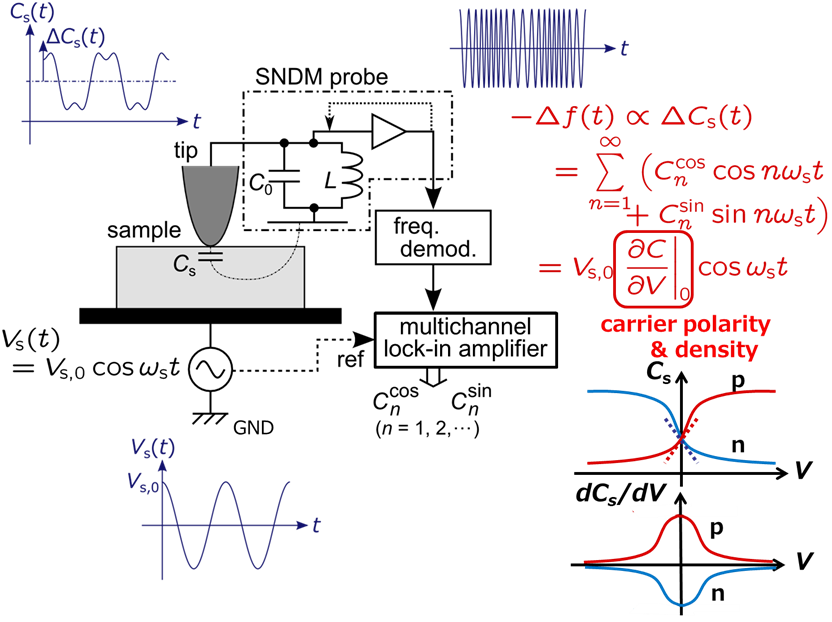
��14��������������Ͷ��Ψ��������Ķ�⼡������������Ͷ��Ψ������ˡ�γ�ǰ�ޡ�
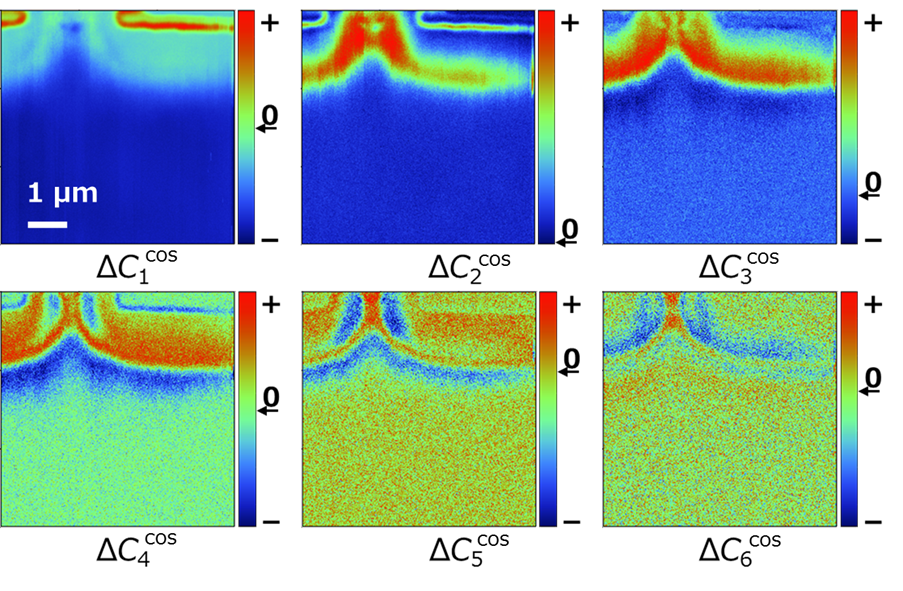
��15��SiC-DIMOSFET�����̤�6�������ι�Ĵ������
��16��ŵ��Ū��C-V������SiC-DIMOSFET�ζ�˳�ؤβĻ벽.
�ɽ�DLTSˡ�ˤ��MOS���̥ȥ�åפ�ʬ�۷�¬
��°-����ʪ-ȾƳ��(MOS)���̤�ʪ��Ū������ȾƳ��MOS�ǥХ����������������礭�ʱƶ���ڤܤ������ߤޤ�MOS���̤γ��̽��Dit�� ��¬������ˡ��Hi-Loˡ��DLTSˡ�Ȥ��ä�MOS����ѥ�������ܤˤ�����ˡ���Ѥ����Ƥ��뤬����������ˡ�ϥȥ�åפ�2����Ū��ʬ�۷�¬�ˤ� Ŭ���Ǥ��ʤ��������������¤Υȥ�åפϳ��̶�˵��2����Ū�ʾ��ˤ�äƤ�3����Ū�ˤ�ʬ�ۤ��Ƥ��뤳�Ȥ��������ʤ����ԶѰ��ʬ�ۤ�MOS���̰� ư���㲼�θ����ˤʤäƤ�������ưפ˿�¬�Ǥ��롥 ������MOS����ѥ����ξ����Ŷˤ������SNDM�ζ�°õ�ˤ��Ѥ��ɽ�Ū��DLTSˡ�ιԤ���ɽ�DLTSˡ���˳�ȯ�������ʾ����Ŷˤ˶˺٤�õ �ˤ��Ѥ�������Ǥ���Τ�ñ��SNDM�ιⴶ�����˰��äƤ��롥�� ��17�ˤ��θ����ޤ����ե���ѥ륹��ȿ�����������������̱�����ο����ȸ���λ�������¬���뤳�Ȥˤ��õ��ľ����Dit���礭���ȥ��ͥ륮���������Τ뤳�Ȥ��Ǥ��롥 �ܼ�ˡ���Ѥ���45-nm������SiO2�����ĥ��ꥳ���̤�4º-off n-�� 4H-SiC �����ϡ���Ditʬ �ۤ��¬��������¬���Ѥ�������ץ��3����� #S-45-1����ץ�ϥɥ饤�����ΤߤΥ���ץ�Ǥ��ꡤ�Ĥ���ĤΥ���ץ��NOʷ�ϵ����POA����(post-oxidation annealing) (POA) ��Ԥä���ΤǤ��롥POA���� 1250�� 10ʬ (#S-45-2)�� 1150�� 60ʬ (#S-45-3)�Ǥ��ꡤ�������ޥ����ʼ�ˡ��ɾ�����줿Dit ��#S-45-1���Ǥ�⤯ #S-45-3 ���Ǥ��㤤. ��18�ˤ���黰�ĤΥ���ץ��ɽ�DLTSˡ��ɾ��������̤���ɾ������Dit�λ�����ʥ��ͥ륮�������������ˤ���1µsec�Ǥ��롥������ʬ����褦��POA�����٤˽��ä�Dit��ʿ���ͤϾ������ʤäƤ��뤬���ɤ����ˤ����Ƥ�Dit��2����Ū��ʬ�ۤ��Ƥ�������ɤ�ʬ���롥 ���Τ褦�˿���ȯ�ζɽ�DLTSˡ��MOS���̤�ɾ���˶ˤ��ͭ���Ǥ��롥
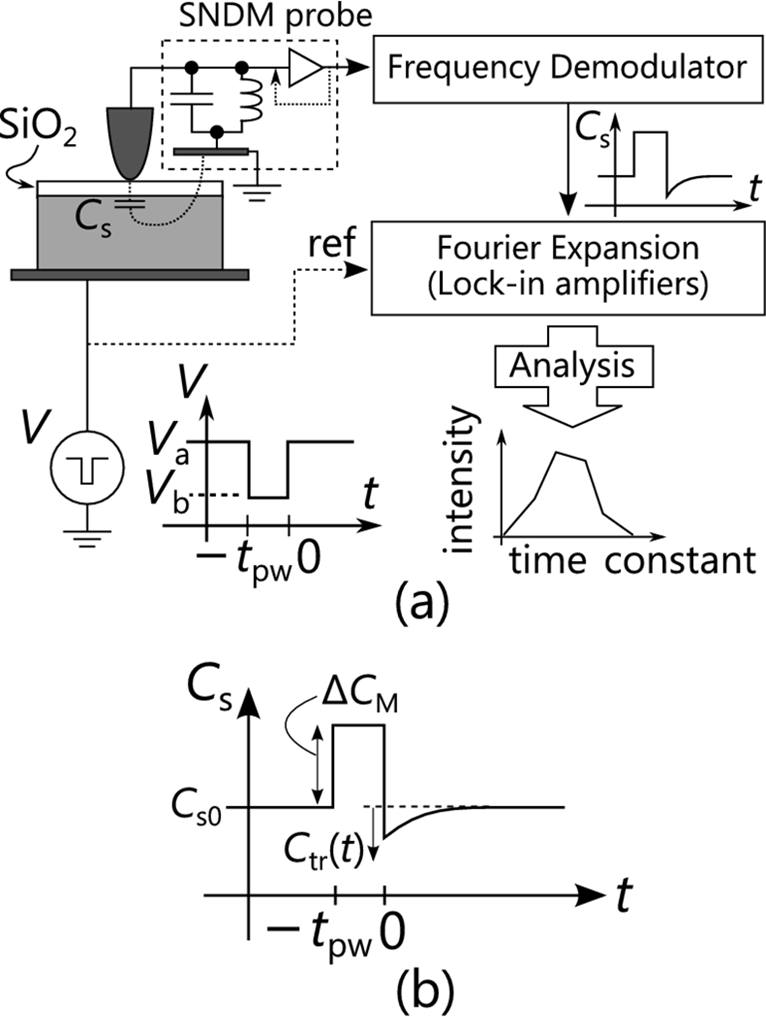
��17���ɽ�DLTSˡ�θ�����. (a) ��¬�ϤΥ֥��å������������(b) ��tpw�Υѥ륹���û��˥ƥ��å�ľ���ǵ���������Ū�����������Ѳ���
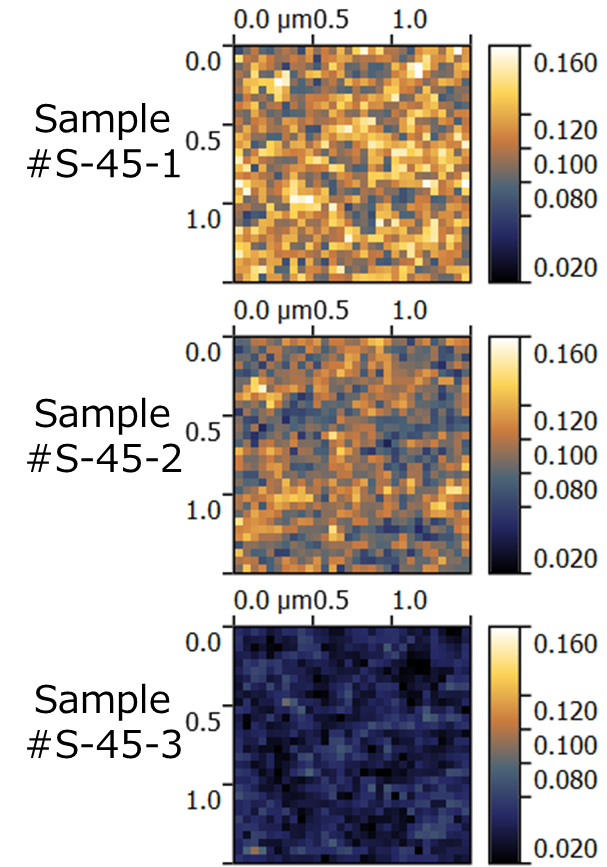
��18��SiC MOS���̤ζɽ�DLTS����@ ��=1µsec��. �Ť���ʬ�����뤤��ʬ�Ϥ��줾��Dit���㤤�ΰ�ڤӹ⤤�ΰ���������롥
����ʬ��SNDM (Tr-SNDM)
���������Ѳ��ι�®����ʬ���¬��ȾƳ����εڤӳ��̤η��ɾ��������ͭ���Ǥ��롥����SNDM���Ѥ��ƥʥΥ�������ζ���ʬ��ǽ���Ļ���ʬ���������̷�¬���Ѥ�ȯ�����ʻ���ʬ��SNDM (Tr-SNDM)�ˡ� SiO2/4H-SiC ���̤˲ä���줿3 ns�Υѥ륹���б����������ʬ���������̱����θ��Ф����������� ������Tr-SNDMˡ��ɽ�DLTSˡ��Ŭ�Ѥ�SiO2/4H-SiC ���̽�̤ι����ʬ��ǽ��¬�ˤ����������������γ��פ�19 ��24�˼���.
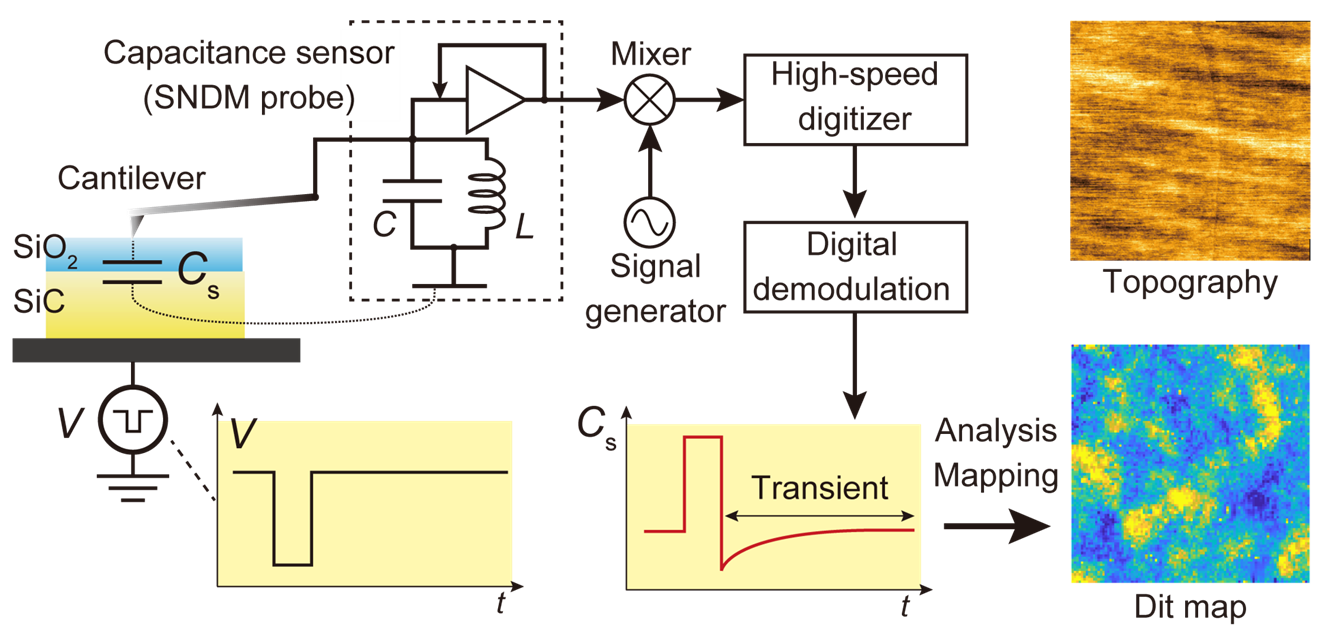
��19������ʬ��SNDM�γ�ǰ�ޡ�
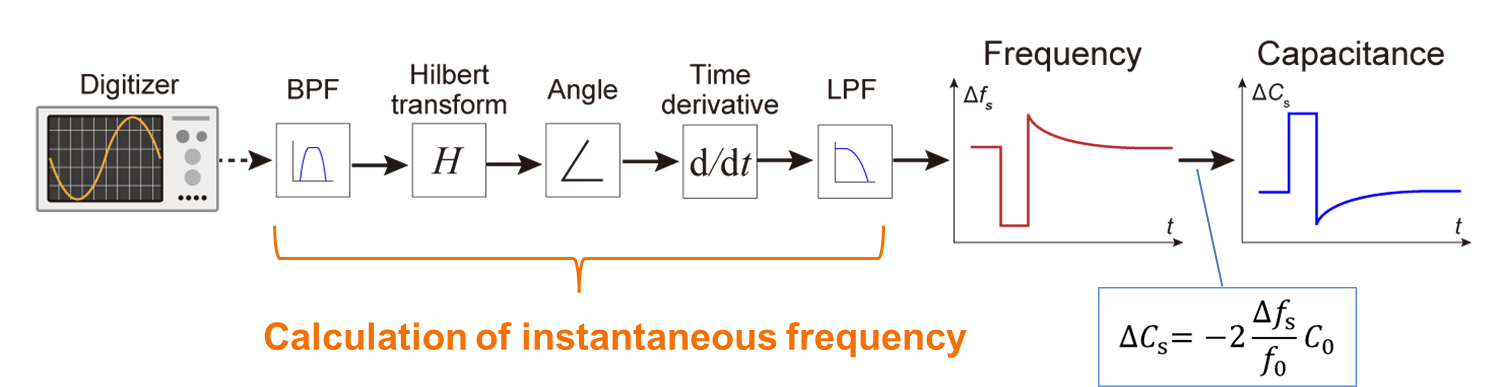
��20��Tr-SNDMˡ���Ѥ��Ƥ���ҥ�٥���Ѵ��ˤ��ֻ����ȿ��ο��ͷ�ˡ��
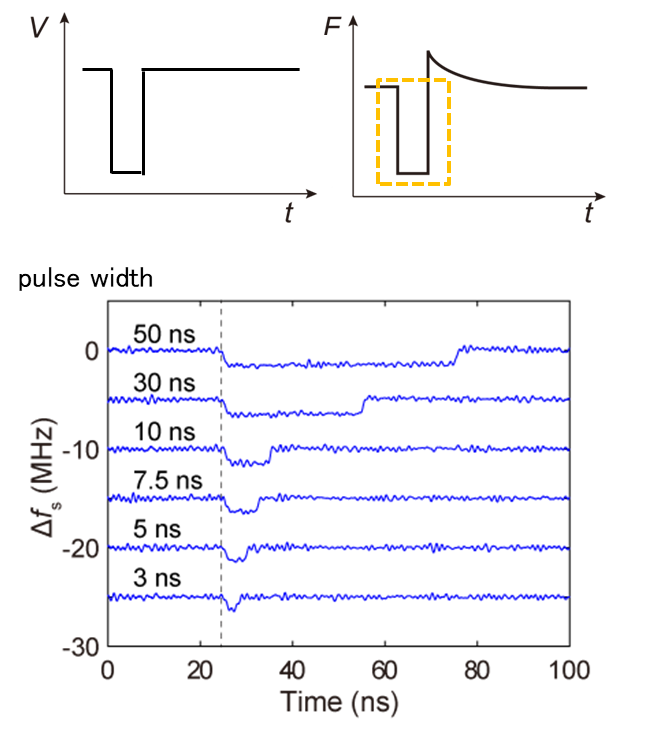
��21��Tr-SNDMˡ������줿����ѥ륹�ȷ����Ф��������Ѳ��ʼ��ȿ��Ѳ��ˤα����ȷ�
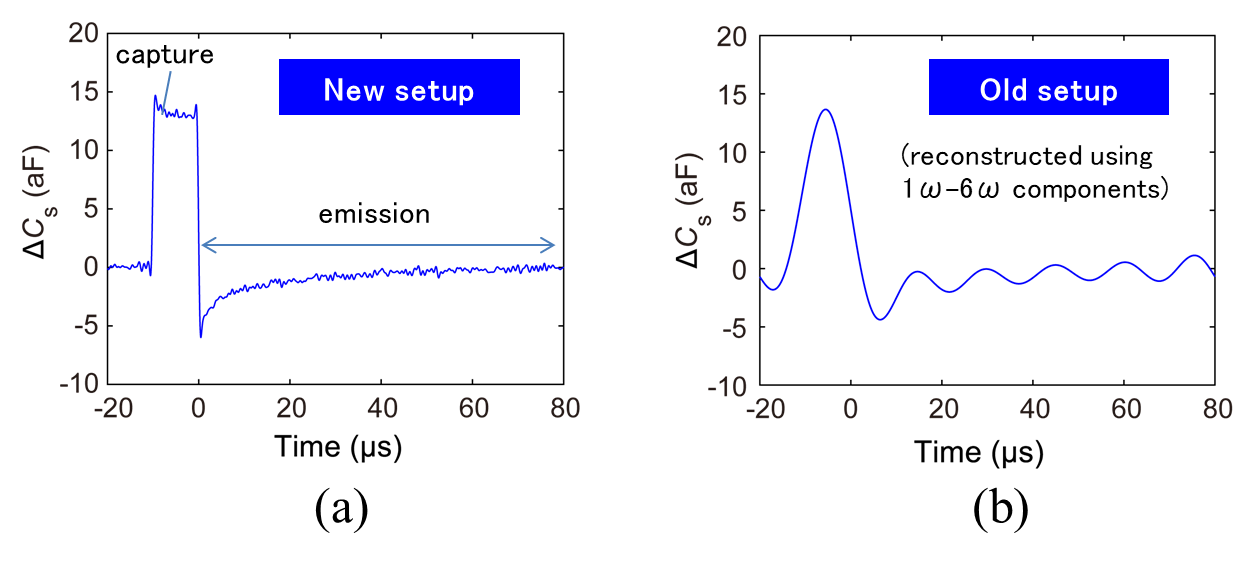
��23�������Ѳ��ȷ������. SiO2/SiC ����ץ��10 µs 10 V�Υե���ѥ륹��ä����Ȥ��έ�Cs�λ����Ѳ�(a) tr-SNDMˡ�ˤ���� (b) FM��Ĵ��ȥޥ������ͥ���å�����פ��Ѥ�������ˡ�ˤ����.
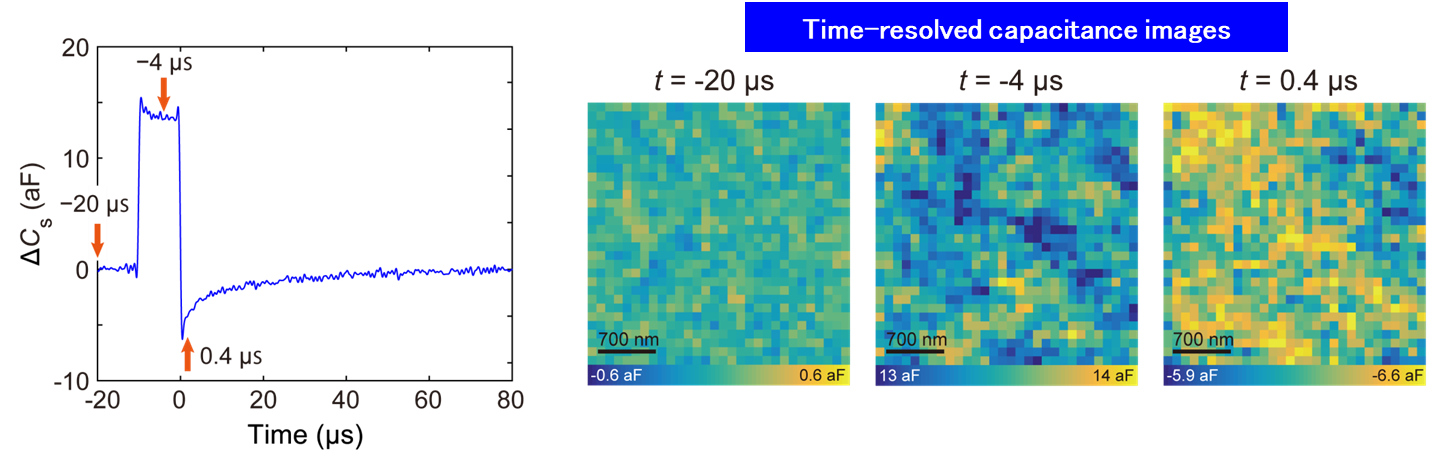
��24��t = -20 µs, t = -4 µs, �ڤ� t = 0.4 µs�Ǥΰ��åѥ륹���Ф������������Ѳ���Cs�� 2������. ��t = -20 µs���ȥ�åפ��ŻҤ���ͤ�������ʤΤǶѰ������t = -4 µs����ͤ��줿�ŻҤξ��ʤ��Ȥ������б�����2��������t = 0.4 µs����ͤ����ŻҤ�ǻ�٤��б�����2��������t = -4 µs�����ȵե���ȥ饹�ȤˤʤäƤ��롥
�����ء�2������ȾƳ�ΤΥ���ꥢʬ�۴ѻ�

��25���˥��֥ɡ��פ��줿SiO2�嵡����Υ��β�����֥ǥ��MoS2�ˤ�SNDM�ѻ���� (a) ������ (b) SNDM��������Υ���ӥ������ϳ����ο��ꤵ�줿�ؿ���ɽ����[Reprinted with permission from Fig. 4, J. Appl. Phys. 128, 074301(2020). Copyright 2020 American Institute of Physics]
SNDM�ϥ��ꥳ���ú�������Ǥʤɤ�ȾƳ�Τ˲ä��ơ��Ƕ�����˸��椵��Ƥ��븶���ء�2������ȾƳ�ΤΥ���ꥢʬ�۴ѻ��ˤ�Ŭ�Ѳ�ǽ�Ǥ�����ǯ������ե���ʤ��ؾ�ʪ����ñ�����ؤޤ���������������ʪ���������ðۤ�ʪ���䤽�ΥǥХ������ѤΤ�������˸��椵��Ƥ��ޤ����ؾ�ʪ���Τʤ��Ǥ⡢��β�����֥ǥ�ʤ�ȾƳ�Τ�������������ȾƳ�Τϡ��������ȾƳ�κ����Ȥ��ƴ��Ԥ���Ƥ��ޤ�����ޤ�Ǯ����Si���ľ�˵���Ū����Υ�����˥��֥ɡ���MoS2��SNDM���Ǥ����˥��֤�p�����Τ���ɡ��פ���Ƥ��ޤ������������ذʲ��Υ˥��֥ɡ���MoS2��p��ȾƳ�ΤȤ��Ƥ��������ݻ����뤫��ɬ�����⼫���ǤϤ���ޤ��ºݡ�SNDM�Ǵѻ������¿����ʬ�ǤϳΤ���p����¿������ꥢ�ʥۡ���ˤ����Ф���������ñ����ʬ�Ǥ�n����¿������ꥢ���Żҡˤ����Ф��줿���Ȥ���ޤ���狼��ޤ����ܤ�����Ƥ��̤��顢�ؿ���10�ذʾ�Ǥϥۡ���̩�٤Ϥۤܰ���Ǥ������ؿ���10�ؤ��ڤ�ȡ����衢¿������ꥢ�Ǥ��ä��Ϥ��Υۡ����̩�٤��������Ϥ��ᡢ2-3�ؤǤϤۤܶ�˳���֤ˡ�ñ�ؤˤʤ�ȤĤ��ˤ��ŻҤ�¿������ꥢ�ˤʤ�p������n���ؤ����ܤ��ͻҤ�SNDM�ѻ��DzĻ벽�Ǥ������Ȥ��狼��ޤ�������Ը���η�̤�դޤ���ȡ�MoS2��ɽ�̤˰տޤ���������ɥʡ��ˤ�äơ��˥��֥ɡ��פθ��̤�������졢�ؿ��������ʤ��ɽ�̤���Υɡ��ԥ��˥��֥ɡ��פθ��̤���äƲ�����Ȥʤꡢ�Ĥ��ˤ�n����������Τȹͤ����ޤ������ꥳ��ʤɤΤ褯�Τ���ȾƳ�ΤȤϰۤʤꡢ������ȾƳ�Τ�������������ˤ��������ϥХ륯����ɽ�̤䳦�̤������˶������������ΤǤ����ޤ���Ʊ��������UV/����������ȸƤФ�������Ԥ��ȡ����ޤ˼����褦�ˡ�ñ�ؤ����Ǥʤ�5�����٤��ؿ��������ʬ�ޤǡ������n�������ʤळ�Ȥ��狼��ޤ����������غ������Ѥ����ȥ�����ʤɤΥǥХ����ץ������Ǥϡ�¿���ι������͡��ʽ�����Ԥ����Ȥ��ͤ����ޤ������ƽ����������Υ���ꥢ̩�٤ˤɤΤ褦�˱ƶ����뤫�����ˤ�뤳�Ȥ�ɬ���Բķ�Ǥ����ܷ�̤ϡ�SNDM�Ǥϸ�����ȾƳ�ΤΥ���ꥢʬ�ۤ�ʥΥ��������ɾ�����뤳�Ȥ���ǽ�ʤ��ᡢ������ȾƳ�ΥǥХ����ΥǥХ����ץ������ڤ��뤿���ͭ�Ѥʼ�ˡ���������뤳�Ȥ��ޤ���
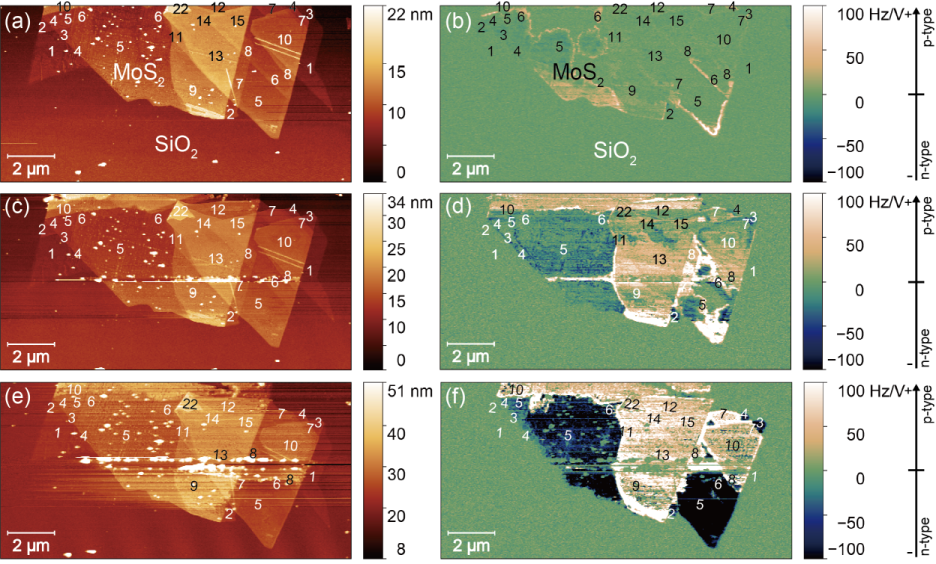
��26����25��Ʊ�������UV/���������������������SNDM�ѻ���̡�(a), (b) ��������10ʬ�� (c), (d) 5ʬ���ɲý�����ʹ��15ʬ�֡� (e), (f) �����5ʬ�ɲý�����ʹ��20ʬ�֡ˡ� (a), (c), (e)�Ϸ����� (b), (d), (f) SNDM����ɽ����[Reprinted with permission from Fig. 6, J. Appl. Phys. 128, 074301(2020). Copyright 2020 American Institute of Physics]
3�����ե�å����������ŻҤȥۡ����ʬ�ۤ�SNDM�ˤ��ѻ�
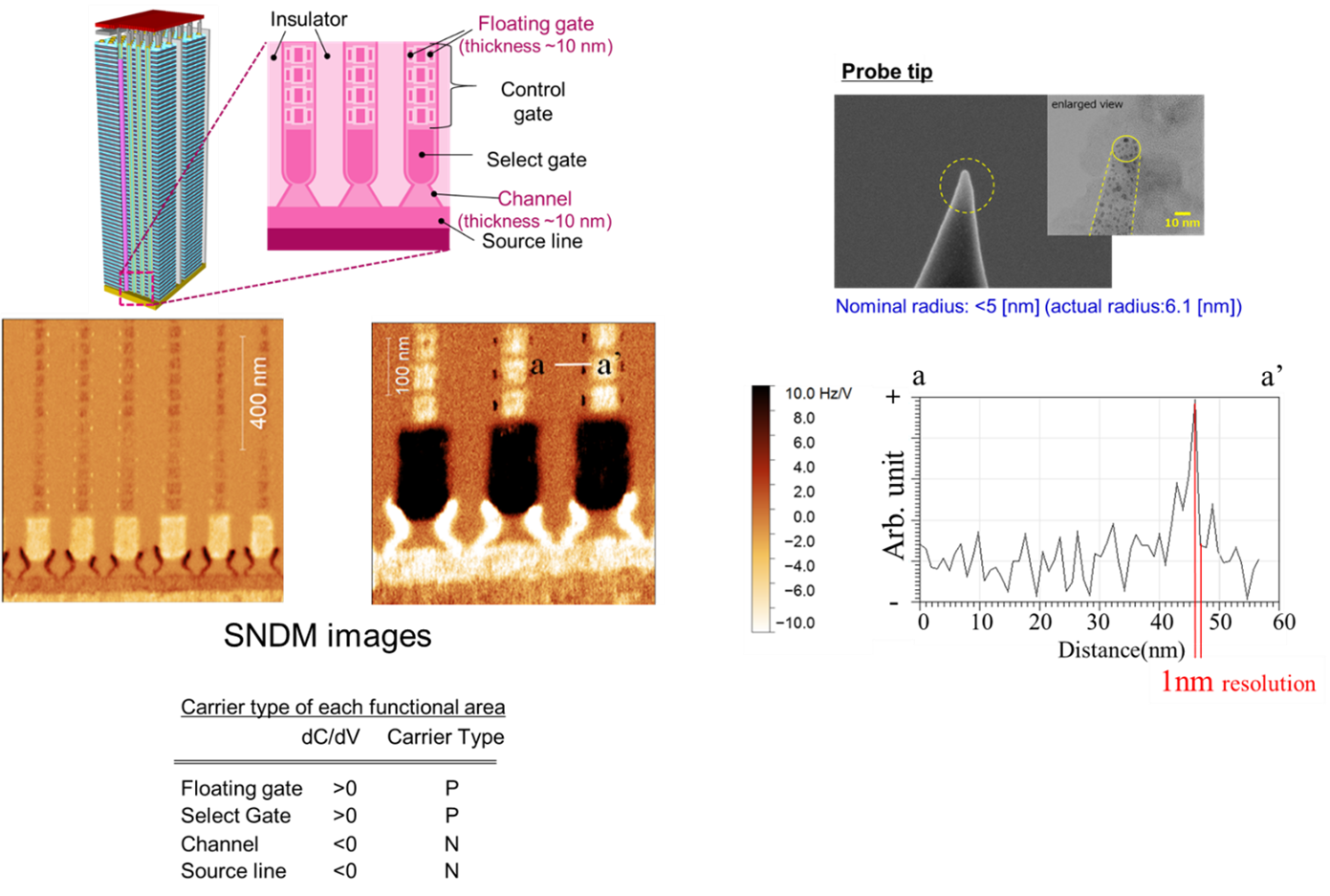
�ǿ��Υե�å�������3�����ʣ�D�˹�¤���뤳�Ȥˤ�äơ��������̤����礵���Ƥ��ޤ��������Ǥϥ�������10 [nm]̤����3D�ե�å�����ꥻ��Υե����ƥ������Ȥ���ӥ���ͥ빽¤�Υ���ꥢʬ�ۤϡ�������������Ͷ���θ�������SNDM�ˤ���Ѥ������Τ�¬�ꤵ�줿��̤Ҳ𤷤ޤ���Ⱦ��<5nm�����˱Ԥ���������ɥ��åפ���Ѥ��ƺǹ�ζ���ʬ��ǽ��ã�������طʤȤΥ���ȥ饹�Ⱥ����礭���ե����ƥ������Ȥ�SNDM�����������뤳�Ȥ��������ޤ������Ǿ�����ʬ��ǽ����ꤷ��SNDM��1.9 [nm]̤���ζ���ʬ��ǽ�����Ȥ��ǧ���ޤ���������ˡ�����ͥ�֤�n���Խ�ʪ�γȻ�Ĺ�κ�(��������)��21 [nm]̤���Ǥ���Ȥ������Τʾڵ��Ĥ��ߤޤ����������η�̤ϡ��ǿ��ζ������ʥǥХ����Υѥե����ޥκ�Ŭ���ȥǥХ����θξ���ϤˤȤä�����ͭ������ˡ���Ω���뤳�Ȥ������������Ȥ��̣���ޤ���
- K. Honda, K. Ishikawa, and Y. Cho: J.Phys.: Conf. Ser. 209 (2010) 012050
- N. Chinone and Y. Cho: IEEE Transactions on Electron Devices 63 (2016) 3165
- K. Hirose, Y. Goto, N. Chinone, and Y. Cho: Jpn. J. Appl. Phys 55 (2016) 08NB13
- K. Hirose, K. Tanahashi, H. Takato, and Y. Cho: Appl. Phys. Lett. 111 (2017) 032101
- N. Chinone and Y. Cho: J. Appl. Phys. 122 (2017) 105701
- Y. Yamagishi and Y. Cho: Appl. Phys. Lett. 111 (2017) 163103
- K. Yamasue and Y. Cho: Appl. Phys. Lett. 112 (2018) 243102
- J. Hirota, K. Yamasue, and Y. Cho: Microelectronics Reliability 114 (2020) 113774

















