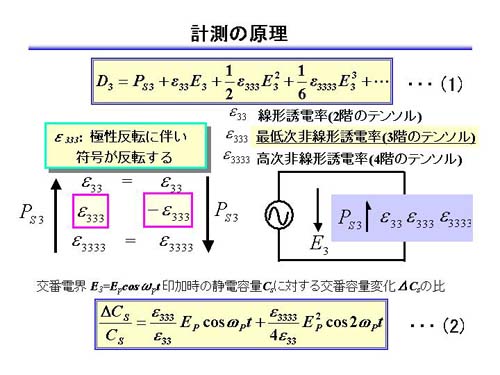
SNDMは,非線形誘電率を測定することによって,分極の方向を判断します.
分極状態が上向きであろうと下向きであろうと,線形の誘電率は変わらないのですが,非線形誘電率は符号がかわるのです.ココに着目しています.
非線形誘電率が存在するということは,その材料に電界をかけると誘電率が変化することを意味しています.
ということは,電界をかけた時,誘電率がどう変化するか(増えるか,減るか)を計測すればいいのです.
簡単のために下図の様な並行平板を考え,Z方向(3方向)の電界のみを考えます.外部から交番電界Epcosωpを印加したとき,元々の容量に対する,微小な容量変化の割合は,下の図の(2)式で与えられます.
よって,印加した交番電界に比例して変化する成分を抜き出すと非線形誘電率ε333が測定できるのです.(もし印加交番電界の2倍の周波数で変化する成分を抜き出すと更に高次の非線形誘電率ε3333が測定できます.)
その誘電率の変化は非常に僅かなのものです(元々の値の100万分の1(10-6)程度です).

それが,可能なのです.容量の変化を周波数の変化に変換してやるのです.
コンデンサをご存じでしょう.コンデンサの静電容量は電極間の誘電率で決まります.また,コイル(L)とコンデンサ(C)を用いたLC共振回路の共振周波数fは次式のように,L,Cの値で決まります.ですから,測定したい材料でコンデンサを形成し,LC発振器を構成すれば容量変化を周波数変化に変換できるのです.
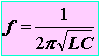
世の中にはいろいろな物理量を測定する装置があるのですが,なかでも周波数を測定する装置は,比較的安価で,かなりの桁数を測定できます.また,周波数はミキシングすることで,変化している桁のところだけを抜き出して計測できるので,元々の周波数が高くても,小さな周波数変化が測定できるのです.
例えば10[GHz](1010[Hz])のBS放送の信号で1KHzの音声信号(103)の情報を抽出できていることを考えれば,納得できると思います.
非線形のある材料に,交番的に変化する電圧を印加しながら,この発振周波数のスペクトラムを調べることで,いろいろなことがわかるのですが,詳しくは省略します.この測定法は,非線形誘電率の動的測定法として,長教授が1992年に開発したオリジナルな計測技術です.
材料を切り出してコンデンサをつくるのは,均一な材料(バルク)の定数を精密に決定するときだけです.
2次元計測には,もっと簡単に,針を当てるだけで即座にコンデンサを形成する方法を用います.つまりプローブを使うのです.
ですから,どのようなプローブを使うか,これが2次元計測では高分解能化のキーポイントになります.
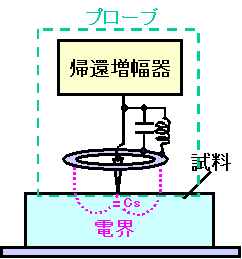
プローブは,リング状のグランド電極と,電界研磨した先端が非常にシャープなニードル,外付けのLとCが帰還増幅器に接続されている構造です.ニードルの先端から試料を貫通してリング電極へたどる電界のパスがありますが,これが容量(コンデンサ)となります.この容量と,LとCにより発振周波数が決まる発振器が構成されています.
試料の誘電率が変わると,ニードルとリング電極間の容量が変化するため,発振周波数が変化する仕組みになっています.
このプローブは,試料表面でコンパクトな構成になっており,10-22[F]という,非常に小さい容量を計測することが可能です.これは,キャパシタンス顕微鏡という装置より,約4桁も微小な容量を測定できるということです.

上図は,プローブの写真です.リングの外形が約7mmです.銀色のケースの中に発振回路が入っています.
上図のプローブを用いると,それだけで,線形の容量(線形の誘電率)を測ることができるのですが,私たちが一番関心あるのは,非線形の誘電率です.それを測るための,測定系のブロックダイアグラムは次のとおりです.
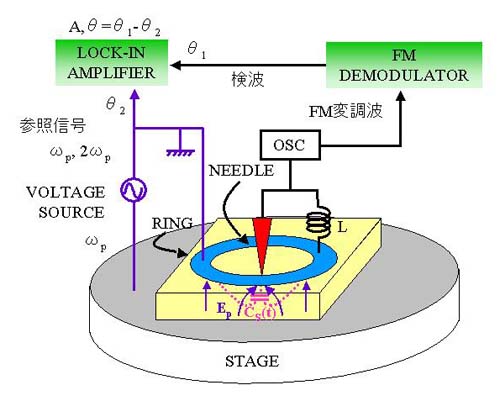
ステージとリング(およびニードル)間に,外部から交番電界Epを印加すると発振器の発振周波数は,Epに伴って変化します.そのときの符号を含めた発振周波数の変化の割合が,ニードル直下の非線形誘電率によって決まります.よって,その変化の割合を,プローブを2次元スキャンしながら計測すればいいわけです.
具体的には,発振周波数の変化をFM復調器で検波した後,ロックインアンプで,印加電界の周波数で同期検波するのです.